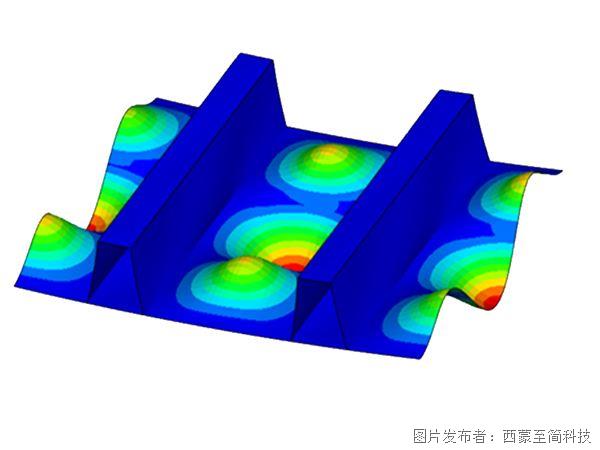
COMSOL網格劃分:有限元分析中的技巧
有限元分析(FEA)是求解工程與物理學問題中廣泛應用的數值分析方法。在進行有限元分析中,網格劃分作為一個基礎而關鍵的步驟,能夠直接影響結果的精確度與計算效率。本文將簡要介紹網格劃分的作用、COMSOL中常見的網格類型及劃分技巧。
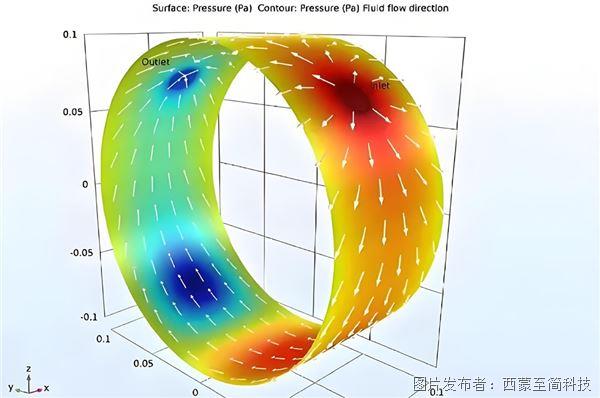
一、為什么要進行有限元劃分網格
在有限元分析中,網格劃分的目標是將連續的物理空間離散化為有限個小單元,從而能夠在每個小單元內使用數學方程進行求解。這種方式可以將復雜問題轉化為易于處理的局部問題。每個小單元可以是多種形狀,如三角形、四邊形、四面體、六面體等,選擇合適的網格類型是影響模型精度和效率的關鍵。
通常來講,越細化的網格越能得到精確的模型,但過于細化的網格會造成計算量和內存需求大幅增加。因此,如何根據需求合理進行網格劃分,是有限元分析中的重要一環。
二、COMSOL網格劃分類型
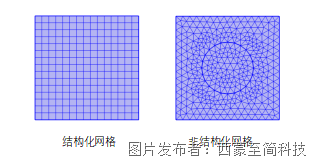
COMSOL的網格劃分主要分為兩大類,即結構化網格和非結構化網格。
結構化操作用于生成規則的結構化網格,COMSOL中國包括映射和掃掠。這種網格適合對稱性較好的問題,能夠降低網格數目,降低計算的復雜度,具有更高的效率。然而,結構化網格只能對形狀相對規則的結構進行劃分,而不適用與復雜結構。
非結構化操作用于生成非結構化網格,包括自由三角形網格、自由四邊形網格、以及自由四面體網格等。其中四面體網格是三維網格生成的唯一選項。這類網格可以對任何幾何結構進行網格劃分,能夠更靈活地適應復雜形狀的邊界,適用于生成復雜幾何形狀或不規則邊界。
在實際應用時,通過合理結合結構化網格和非結構化網格,在需要精細劃分的區域使用細網格,而在相對平坦或規則的區域使用粗網格,從而更好地平衡計算效率和精度需求。
三、COMSOL網格劃分方式
COMSOL提供了依據物理場生成網格和用戶手動控制網格的方法。
物理場控制網格劃分會根據以及設置好的物理場自動適配,在合適的區域劃分合適的網格類型和大小,如熱傳導、流體力學、結構力學等物理場中,COMSOL會根據物理特性自動優化網格劃分。
對于更復雜的模型,用戶控制的網格劃分可以根據模型的具體需求手動調整網格類型和大小。對于特定的物理場問題,尤其是在模擬細節要求較高的部分,用戶可以手動設置網格大小和類型,確保網格能夠合理覆蓋需要精細計算的區域,提高計算結果的準確性。
四、COMSOL網格劃分技巧
網格的精細程度直接影響計算結果的準確性和計算效率,在一個理想的有限元模型中,網格應該細化得足夠精確,以便能夠捕捉到系統的細微變化。然而,細化網格的同時也會帶來更大的計算量。在實際應用中,網格的劃分往往采取漸進的策略。
初始解:
在分析的初始階段,可以通過使用粗網格快速得到初始解。粗網格雖然網格較大,精度較低,但單元少,計算速度快,可以用于判斷載荷即約束等條件是否正確施加,對模型進行初步估計和快速評估。隨后通過對粗網格模型的判斷,逐步細化網格以提高精度。
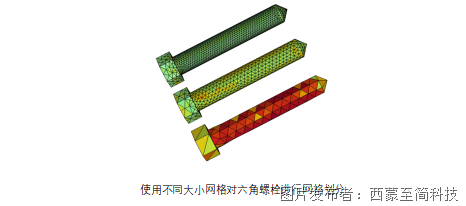
劇烈變化區域:
對于物理場中變化劇烈、數值突變的區域,如尖角、裂紋、材料分界等應特別注意細化網格。這些區域可能會存在較大的應力集中或溫度梯度,粗網格無法準確捕捉這些變化,從而帶來不準確的計算結果。
物理場分界:
在不同的物理場分界處,網格應該更加密集。因為不同材料的性質或物理場的行為在交界面附近會發生明顯變化,粗網格往往難以捕捉到這些變化。可以通過手動設置網格大小,確保物理分界處的網格足夠精細。
均勻區域:
在物理場變化較小的區域,可以采用較粗的網格劃分,粗網格能夠有效減少計算的時間與內存消耗,適用于對精度要求較低的區域,從而減少計算量,提高計算效率。
五、總結
網格劃分是有限元分析中的重要一環,合理的網格劃分不僅能夠確保結果的精度,還能有效控制計算資源的消耗。通過根據物理場的特點手動調整網格大小,在變化劇烈或物理分界處進行精細劃分,可以顯著提高計算結果的準確性和可靠性。在進行有限元分析時,確保合理劃分網格、選擇合適的網格類型和劃分技巧,可以獲得更加精確且高效的計算結果。
提交
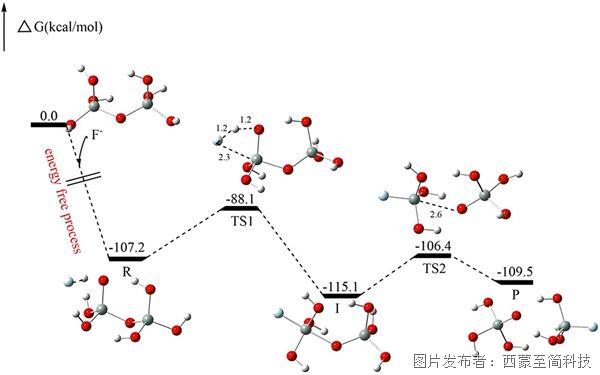
量化計算中:過渡態理論的起源和意義
有限元仿真中的穩態和瞬態是怎么回事?
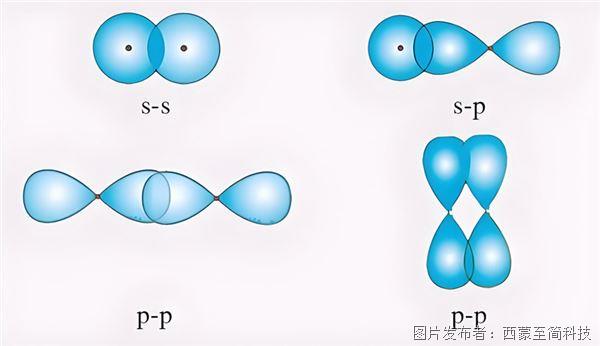
量子化學中的價鍵理論
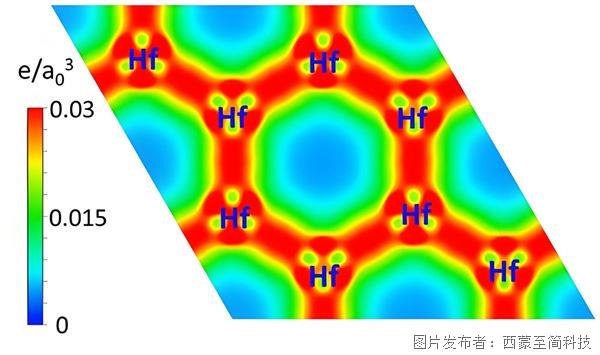
量子化學:材料的電子態密度
VASP最全入門干貨:四個輸入文件詳解








 投訴建議
投訴建議